なんでメジャーの３音は低くとるか、知ってる？【純正律と平均律のおはなし】

こういうチューナーって、今でも使うんですかね。

僕が吹奏楽部だった10年以上前(かなしい🥺)は、もう必需品。合奏に忘れようもんなら、先生にバレないように隣の子に貸してもらったものです…懐かしい。

今や、チューナーすらもスマホアプリでできる時代なので、そんな文化もないの…?とか考えてます、どうもはらいちですお願いします。

さて、吹奏楽部の皆さんなら、「純正律」って聞いたことありますかね。

僕も中1の頃に先輩に教わって初めて知ったのですが、

ドミソをピアノで弾いても、実は綺麗なハーモニーじゃない！！

綺麗にするには、ミの音をちょっと低くしないといけない！！(ソもほんのちょっと高くしないといけない！！)

と知ったとき、僕は雷を打たれたような衝撃を受けましたね。

小さい頃ほんのちょっとピアノをやっていた僕にとって、”ドレミファソラシド”という揺るぎない音階、音程。

ドミソ、ファラド、ソシレ。揺るぎない完璧で綺麗な和音。

そう疑いもなく信じていた僕にとって、純正律という概念は意味がわかりませんでした。

というか、音楽やってない人からしたら意味わからないですよね、コレ。

もしかしたら、音楽やってても純正律という概念を知らない人も結構いそう。

実際、中学生の僕も意味がわからず、

ほーん、ドミソのミのときはちょっと低くすればええのな。

あ、ドミbソとかの短調のときのミbは高くするんだ。へんなの、そういうもん？？

というくらいでした。

ということで今回は、昔の自分でもわかるように、

なんでそんな面倒なことをしないといけないか？？という話をして行きますよ。

まずは、体感しましょうか。平均律と純正律。

とてもいい動画を見つけたので、まずはこちらを聞いてみましょう。ちょーわかりやすい。こんな違うんかってなります。

平均律ってなんやねん。

上の動画の冒頭で、とっっっても面白いことを言っていました。

みてない方のために説明すると…

調べてみたら、24セントもずれていたんです(100セント違うとちょうど半音の差になるので、結構ずれてる)。

ここに、純正律と平均律のキモとキモさが凝縮されているのです。

ちょっと確かめてみましょうか。本当に24セント違うか。

興味なかったら次の見出しまで無視してOKです。

最初のドの振動数を、100Hzとしましょうか(実際は違いますが問題ありません)。

ソが1.5倍の150Hz、レがその1.5倍の225Hz…というふうにやっていくと、戻ってくるドは約12974.6Hzになります。(正確には100×1.5¹²Hzです)

最初のドと最後のドは7オクターブ違います。

(家に88鍵のピアノがある人は、いっちばん左のドからはじめて、完全五度で右に進んでみてください、いっちばん端っこのドに帰ってきます!)

1オクターブ上の音は、振動数が2倍になります。

なので、7オクターブ違うと、128倍振動数が違う。つまり、最初のドが100Hzの時、最後のドは12800Hzのはずです。….

お。

完全5度を経てたどり着いたドは、12974.6Hzでしたね。

なのに、オクターブ(完全8度)を経たドは、12800Hz。

ぜんぜんちがーう。

実際これは24セントずれているんです。
それを確かめるには下のちょっと難しい式を使います(みたい人はみてね)。

セントとは、ある音の振動数の、基準となる音とのズレを表します。
ちょうど半音ずれているときのズレを100として表します。

ある音A(Hz)が、基準となる音B(Hz)とどのくらいズレてるかをセントで表す時、以下の式を使います(導出はメンドイので省きますが、¹²√2とか出てきて面白いです。)。

音のズレ具合(セント)=1200×log₂(A/B)

上の、12800Hzと12974.6Hzを代入してみると、
1200×log₂(12974.6/12800)=23.455…となり、12975Hzの方が、12800Hzと比べて約23.5セントずれている(高い)ことがわかります。
(チューナーってこんなむずい計算してたんですね…)

(この約23.5セントのズレは、ピタゴラスコンマ、と呼ばれています。ぜひググってみてね。)

さて、気を取り直して。

めでたく、ちゃんと24セントずれていることがわかったところで。

ドとソは、振動数の比が2:3で綺麗。

ドと1オクターブ上のドも、振動数の比が1:2で綺麗。

なのに、上の計算でもわかったように、この2つはどうあがいても噛み合わない、、、という問題が起こってるんです。

(ここでいう、綺麗というのは、純正律としての完璧な響きのことですよ。)

さあどうしようということで、ピタゴラスをはじめとするいろいろな数学者が悩んだ結果、

めちゃくちゃ平たくいうと、オクターブの振動比である[1:2]、これがズレるのが一番やばいから、これに合わせちゃお、

ということになりました(実際もっとごちゃっとしてるので色々語弊ありそうだけど、こんな理解で十分です)。

要は、1オクターブ上の振動数は2倍になって、間に12個の半音を挟むから、12等分に割っちゃおう！

まあ、そうするとドとソの振動比が2:3じゃなくなっちゃうけど….そこまで気にならないし、妥協した感はあるけどアリっしょ！！

ということです。

均等というと、誤解が生まれかねないのでちょっと補足。

ある音が1200Hzだとそのオクターブ上は2400Hzになりますが、12等分だから1200,1300,1400,…,2300,2400Hzという単純な話ではないのです。

振動数と音の高さは指数関数の関係なので、単純に振動数を12で割っちゃマズいのです。

じゃあどうしてるかというと、半音1個上がったとき振動数を¹²√2倍(1.0595倍くらい)してあげれば、半音12個分で(¹²√2)¹²＝2になってめでたくオクターブになるので均等に12等分できたことになります。

そう、上の動画でも触れられていますが、平均律は妥協の末に生まれたものなんです。

下のドと上のドのウネリを無くそうとした結果、

ドに対するソや、ミ、ミbなど、、、(いや、ド以外の全部。)

の完璧に綺麗な純正律の和音が犠牲になったのだ、、、、

と言うのが、平均律の生まれ持った運命なのです。

だから、平均律で作る和音って、もともと綺麗な和音じゃない。

だから、吹奏楽や管弦楽など、簡単に音程をずらせる場合には、本来の完璧な純正律の響きに戻してあげてるんです。

あえて音程を悪い方にずらしてるわけじゃないんです。

だって、平均律がもうズレてんだもん。既に。

(余談ですが、ピアノなど平均律で調律してある楽器を含む音楽形態では、純正律など考えなくてよくなります。吹奏楽からビッグバンドはじめて、一番びっくりしたのはここ。)

じゃあ、どのくらいズレ修正しないといけないの？？

というと、このくらい。

ルート以外全部やんけ！といいたくなりますが、

平均律が、どれだけの思いで妥協してるかが伝わってきますね…

これは、Bbに対する表ですが、よくみると…

Bbに対するメジャーの3音であるDは、13.7セント低くとる。

Bbに対するマイナーの3音であるDb(C#)は、15.6セント高くとる。

さーて、最初のチューナーの画像をよーくみてみましょう。

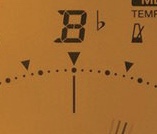
0の左右に、不気味な位置の▼が2つありますねぇ。

小さい⚫︎ごとに2.5セントずつ、大きい●ごとに10セントずつズレるから、、、

勘の良い人はお分かりですね。

左の▼は-13.7セント、右の▼は+15.6セントにちゃーんとなってる！！

(これ、吹奏楽部入って１年くらい、なんで左右非対称なとこに▼あんだろ、へんなの、としか思ってなかったなんて言えない)

あとよく使うのは、

完全五度の+2.0セント、長7度の-11.7セント、短7度の+17.9セントくらいでしょうか。

ちょっと補足。

ちょっと別角度からも話してみます。

平均律は、半音どうしの振動数比は、どこもずっと¹²√2倍(≒1.0595倍)で一定です。

なので、オクターブなら純正律と平均律ともに振動数比は1:2になるのですが、

ドとソだと(純正律では綺麗な2:3でした)、平均律では振動数比は1:(¹²√2)⁷=2:2.9966になり、綺麗な2:3とちょっとズレちゃうのです。

冒頭では、ドとソが2:3で、オクターブが1:2だと言いましたが、ちょっと他の音との振動数比もまとめてみましょう。

ドと…	純正律での振動数比 (左はドの振動数の値)	平均律での振動数比 (左はドの振動数の値)
ド#	15：16	15：15.8919
レ	8：9	8：8.9797
ミb	5：6	5：5.9460
ミ	4：5	4：5.0397
ファ	3：4	3：4.0045
ファ#	32：45	32：45.2548
ソ	2：3	2：2.9966
ソ#	5：8	5：7.9370
ラ	3：5	3：5.0453
シb	5：9	5：8.9090
シ	8：15	8：15.1020
上のド	1：2	1：2

いやー、とても興味深いですね。

平均律の方は、¹²√2という無理数を何回もかけてるだけなのに、こんなに綺麗な整数比に近付いてるとこが面白い。

先ほどのこの表(↓)の値の増減と、上の表がちゃんと対応してるのもポイントです。

（ドとレの場合、平均律だと8：8.9797と純正律の8：9よりちょっと足りないので3.9セント高くとる、逆にドとシの場合は8:15よりオーバーしちゃってるので11.7セント低くとる、みたいな。)

さらにこの表から、純正律の時の、3和音の振動数の比率もわかってしまいます。

こんな感じ。

メジャーの和音(ドミソ)….4：5：6

マイナーの和音(ドミbソ)….10：12：15

sus4の和音(ドファソ)….6：8：9

augの和音(ドミソ#)…20：25：32

dimの和音(ドミbソb)…160：192：225

メジャーセブンスの和音(ドミソシ)…8：10：12：15

セブンスの和音(ドミソシb)…20：25：30：36

こうみると、綺麗な響きほど、比に出てくる数字が小さいって言えそうじゃないですか？

これってめちゃくちゃ面白くて、

「人間が綺麗と思う響き」っていうモヤモヤとした概念だったのに、数学的にも綺麗だ、と証明されてることになるんですよ。

…と、ちょっと熱くなってしまいましたが、

こんな綺麗な比率の和音も、純正律あってのもの。

平均律の場合、どの和音もすべての比に¹²√2とかいう無理数の倍数が出てくるので、こんな綺麗な整数にはなりえません。

(平均律のドミソの場合、1：¹²√(2⁴)：¹²√(2⁷)なので4:5:6ではなく4：5.0397：5.9932になってしまいます。)

この平均律のズレを修正するために、吹奏楽部は頑張って純正律に直しているのです。

決して、純正律にするために音程をずらしてるわけじゃない、ということだけ覚えておいてくださいね。

ただ、今日の話を覚えておくと、

「ほーん、3音は低くするのね〜」とだけ思っていた昔の僕とは違い、

パート練や合奏、アンサンブルなどでめちゃくちゃ応用が効くようになります。

純正律の響きを制したものがハーモニーを制し、ひいてはコンクールの結果やうまさに直結します。

ここに書いてあった話を、何も言わず部活の友人に説明できますか？？？？？

何度も読み返しては、人に説明できるくらいにマスターしちゃいましょう。

では〜！